https://www.acmicpc.net/problem/17386
17386번: 선분 교차 1
첫째 줄에 L1의 양 끝 점 x1, y1, x2, y2가, 둘째 줄에 L2의 양 끝 점 x3, y3, x4, y4가 주어진다. 세 점이 일직선 위에 있는 경우는 없다.
www.acmicpc.net

💡 주의 사항
2차원 좌표 평면 위의 두 선분 L1, L2가 주어졌을 때, 두 선분이 교차하는지 아닌지 알아보기
- 선 L1 : x1, y1, x2, y2
- 선 L2 : x3, y3, x4, y4
- 1,000,000 <= x1, x2, x3, x4, y1, y2, y3, y4 <= 1,000,000이며, 변수는 모두 정수
- L1과 L2가 교차하면 1, L2와 L2가 교차하지 않으면 0

🗒 풀이
일단 집에 있는 수학책을 찾아 다음과 같은 공식을 찾아냈다.

위의 조건들을 활용하기 위해, 두 케이스에 대한 직선의 방정식을 구했다.

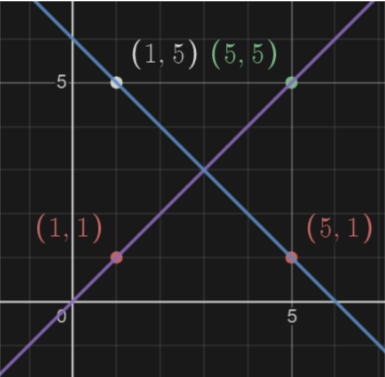
위의 조건들을 갖고 첫번째 케이스에 L1 : (1, 5), (5, 1)과 L2: (1, 1), (5, 5)에 대입했다.
L1은 \( y=-x+6 \), L2는 \( y=x\)로 위의 1번 조건(\( m \neq m' \))에 해당하여 만날 조건이 성사되었다.
하지만 두번째 가정에서 어긋났다.
L1: (1, 1), (5, 5), L2: (6, 10), (10,6)을 지난다고 가정했을 때, 두 점을 지나는 직선이라고 가정한다면 위의 조건이 성립하지만, 선분이기 때문에 두 선분은 만나지 않았다.
직선은 기울기가 다르기만 하면(평행하지 않을 때면) 교차하게 되는데, 선분이라 길이가 정해져 있는걸 간과했다.
그래서 다른 방법을 고민했다.
위 가정에서 좀 더 확대하여 생각해보았다.
만약, 둘 다 선분이라고 가정하지 말고, 하나의 직선과 하나의 선분으로 이루어졌다고 생각해보자.
직선 하나가 다른 선분을 둘로 나누면 만난다고 생각할 수 있지 않을까?

즉, L1과 L2의 선분을 확장한 직선을 직선1, 직선2라고 가정하자.
직선1에 의해 L2가 나누어진다면, 또 반대로 직선2에 의해 L1이 둘로 나누어진다면 둘은 만나다고 할 수 있지 않겠냐는 것이다.
처음 가정에서 확대하여, 두 기울기가 서로 다르면, 즉 곱한 두 기울기가 0보다 작으면 직선 두개는 만난다고 볼 수 있겠다. (f(x)=0라는 직선이 있다고 할 때, 두 점을 각각 넣어 기울기가 반대인 것을 확인하면 된다.)
그러니까 직선을 기준으로 각각 반대 방향에 있으면 되지 않나?

직선이라고 정한 선분을 기준으로 직선의 방정식을 구했고, 나머지 선분의 양 끝 점을 직선의 방정식에 대입했다.
첫번째 케이스에서는 직선을 기준으로 다른 선분의 양 끝점이 하나는 직선 위(+), 하나는 직선 아래(-)에 위치했고, 대입을 해서 값을 얻어 냈을 때 하나는 양수, 하나는 음수로 나와 곱했을 때 음수가 나오는 것을 확인했다. 반대도 마찬가지였다.
하지만 두번째 케이스에서는 한 경우에는 직선을 기준으로 선분이 위와 아래에 배치됐지만, 다른 한 경우에는 직선을 기준으로 선분의 양 끝점이 모두 음의 방향에 위치하는 것을 볼 수 있었다.
이를 토대로 코드를 짜기 위해 식을 정리한 것이 다음과 같다.

def does_it_divide(x1, y1, x2, y2, x3, y3, x4, y4):
f1 = (y3-y1)*(x2-x1) - (x3-x1)*(y2-y1)
f2 = (y4-y1)*(x2-x1) - (x4-x1)*(y2-y1)
if f1 * f2 < 0:
return True
else:
return False
def does_it_intersect():
x1, y1, x2, y2 = map(int, input().split())
x3, y3, x4, y4 = map(int, input().split())
result1 = does_it_divide(x1, y1, x2, y2, x3, y3, x4, y4)
result2 = does_it_divide(x3, y3, x4, y4, x1, y1, x2, y2)
if result1 and result2:
return 1
else:
return 0
if __name__ == '__main__':
print(does_it_intersect())
'알고리즘' 카테고리의 다른 글
| [백준] 2438번: 별 찍기 - 1(java, python) (0) | 2022.07.03 |
|---|---|
| [백준] 1546번: 평균 (java, python) (0) | 2022.07.02 |
| [백준] 1157번: 단어 공부 (java, python) (0) | 2022.07.01 |
| [백준] 1152번: 단어의 개수(java, python) (0) | 2022.07.01 |
| [백준] 1008번: A/B (java, python) (0) | 2022.07.01 |



